Support
Please support me if you like this page. If you buy something using my Amazon link, as an Amazon affiliate I earn a commission.
Result

How the Derivative Calculator Works
For those with a technical background, the following section explains how the Derivative Calculator works.
First, a parser analyzes the mathematical function. It transforms it into a form that is better understandable by a computer, namely a tree (see figure below). In doing this, the Derivative Calculator has to respect the order of operations. A specialty in mathematical expressions is that the multiplication sign can be left out sometimes, for example we write 5x instead of 5*x. The Derivative Calculator has to detect these cases and insert the multiplication sign.
The parser is implemented in JavaScript, based on the Shunting-yard algorithm, and can run directly in the browser. This allows for quick feedback while typing by transforming the tree into LaTeX code. MathJax takes care of displaying it in the browser.
When the "Go!" button is clicked, the Derivative Calculator sends the mathematical function and the settings (differentiation variable and order) to the server, where it is analyzed again. This time, the function gets transformed into a form that can be understood by the computer algebra system Maxima.
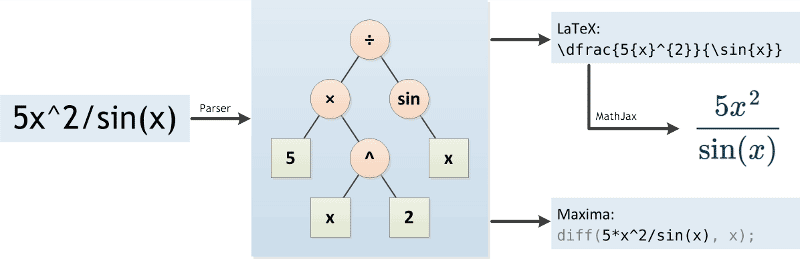
Maxima takes care of actually computing the derivative of the mathematical function. Like any computer algebra system, it applies a number of rules to simplify the function and calculate the derivatives according to the commonly known differentiation rules. Maxima's output is transformed to LaTeX again and is then presented to the user.
Displaying the steps of calculation is a bit more involved, because the Derivative Calculator can't completely depend on Maxima for this task. Instead, the derivatives have to be calculated manually step by step. The rules of differentiation (product rule, quotient rule, chain rule, …) have been implemented in JavaScript code. There is also a table of derivative functions for the trigonometric functions and the square root, logarithm and exponential function. In each calculation step, one differentiation operation is carried out or rewritten. For example, constant factors are pulled out of differentiation operations and sums are split up (sum rule). This, and general simplifications, is done by Maxima. For each calculated derivative, the LaTeX representations of the resulting mathematical expressions are tagged in the HTML code so that highlighting is possible.
The "Check answer" feature has to solve the difficult task of determining whether two mathematical expressions are equivalent. Their difference is computed and simplified as far as possible using Maxima. For example, this involves writing trigonometric/hyperbolic functions in their exponential forms. If it can be shown that the difference simplifies to zero, the task is solved. Otherwise, a probabilistic algorithm is applied that evaluates and compares both functions at randomly chosen places.
The interactive function graphs are computed in the browser and displayed within a canvas element (HTML5). For each function to be graphed, the calculator creates a JavaScript function, which is then evaluated in small steps in order to draw the graph. While graphing, singularities (e.g. poles) are detected and treated specially. The gesture control is implemented using Hammer.js.
If you have any questions or ideas for improvements to the Derivative Calculator, don't hesitate to write me an e-mail.